CS210 Tutorial 9
Complete the following exercises pasted below:
Q1. Create a binary search tree (BST) representation for the following input. The element data type in each node is int.
8 11 7 4 2 6 17 13 12 14 7 5 10 9 15 13 1 18 19 17 9
Q2. Suppose that we have numbers between 1 and 1000 in a binary search tree, and we want to search for the number 363. Which of the following sequences could not be the sequence of nodes examined?
2,252,401,398,330,344,397,363.
924, 220, 911, 244, 898, 258, 362, 363.
925, 202, 911, 240, 912, 245, 363.
2,399,387,219,266,382,381,278,
935, 278, 347, 621, 299, 392, 358, 363.
Q3. 12, 44, 13, 88, 23, 94, 11, 39, 20, 16, and 5,
Build a Binary Search Tree using the above keys.
Q4. Remove the following keys from the above BST. Indicate which case for removal applies (0) no children; (1) one child; (2) children.
20, 23, 44, 5, 12, 88.
Q5. What is the run time for best case and worst case scenarios for BST. Show using examples.
Q6. Build a BST of characters using the following input
A, B, C, D, E, F, G, H, I, J
What is wrong with this tree?
Q7. Build a BST of characters for the following set of input
M, D, B, C, A, Y, X, Z
How many comparisons to search Z?
Scroll down for solution!
Solution
Q1 - Q4. Please use the Visualgo.net to type in the values. It will create the BST for you!
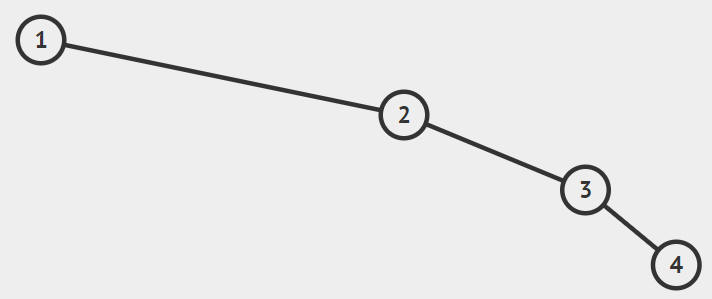
Q5. Best case scenario for insertion is, if the tree is empty, it takes only O(1) time to insert a node. On average, BST gives a O(log n) time. Worst case scenario occurs when the tree appears as a linked list. In the BST pasted below; to insert 5, we need to traverse n nodes to insert to the right of 4; this gives the worst case scenario with O(n).

Q6. The BST will appear as follows:
A
\
B
\
C
\
D
\
E
\
F
\
... and on.
This is also a lopisided tree which will give a worstcase scenario of O(n)
runtime.
Q7. BST for M, D, B, C, A, Y, X, Z would be:
M
/ \
D Y
/ / \
B X Z
/
C
/
A
Searching for Z will take 3 comparisons starting at root M.